libreta chatarra

31.5.18

hasta acá llegamos

El 17 de noviembre de 2003 empezamos este camino experimental del blog. Con un comentario sobre la participación de los Pumas en el Mundial, pasados 7 minutos de las 10 de la mañana.

En principio, era un blog derivado de un sitio, “Super Chatarra Special” (http://superchatarra.com.ar), con actualización mensual. Luego, desde marzo del 2005, el blog tomó el lugar del sitio y empezamos a actualizarlo con frecuencia casi diaria. En este viaje, más de 3 millones y medios de visitas en casi 15 años, relevando la cultura, la política, el deporte. Compartimos historias, chistes, noticias, fotos. Opinamos y opinaron. Hoy el viaje está llegando al final.

Algunos problemas menores de salud, aconsejan no estar tanto tiempo al frente de una pantalla de computadora. Así que es el momento de plantar bandera y dejar acá la aventura de “Libreta Chatarra”. Espero que la hayan disfrutado, como lo disfruté yo. Sólo queda agradecer a todos aquellos que nos difundieron, los que fueron fieles visitantes, los que comentaron nuestras críticas de cine, los que nos siguieron todo este tiempo. Hemos hecho amigos, que espero que se mantengan a la distancia.

Punto final para “Libreta Chatarra”. Fue un gusto recorrer este camino.

Para los que quieran seguir en contacto, pueden seguirme por la cuenta en Twitter: @libretachatarra donde seguiremos compartiendo artículos periodísticos, fotos, arte, opiniones, con un ritmo más light y menos periódico. En ese canal podrán seguirme el rastro.

Un abrazo a todos y gracias por estar todo este tiempo. Hasta siempre.

25.5.18

frases de “Deadpool 2”

¡Qué oscuro! ¿Estás seguro de que no eres del Universo DC?

-¿Quién eres?
-Soy Batman.

-Tenemos reglas. No eres juez, jurado o verdugo.
-¡A la mierda con tus reglas! Lucho por lo que es correcto. Y algunas veces tienes que pelear sucio.

¡Jódete, Wolverine! Primero jode con la clasificación “Prohibido para menores de 18”, y luego, ese hijo de puta peludo sube la apuesta al morir. ¡Qué estúpido! Bueno, ¿adivina qué, Wolvie? Me estoy muriendo en esta película.

¿Sabes lo que tenemos que hacer? Necesitamos construir un maldito equipo. Los necesitamos duros, moralmente flexibles y lo suficientemente jóvenes para que puedan llevar esta franquicia unos 10 o 12 años.

-Mi cuerpo es un instrumento de muerte.
-Ahora no, Dopinder.

Sólo los mejores amigos ejecutan pedófilos juntos.

Con este collar puesto, mi superpoder es sólo un cáncer desenfrenado. Dame un arco y una flecha y soy básicamente Hawkeye.

Lo siento, llegué tarde. Había un grupo de niños discapacitados atrapados en un árbol…

Tienes razón. Estaba peleando con un tipo rudo, pero luego descubrimos que su madre se llama Martha también.

Los niños nos dan la oportunidad de ser mejores de lo que solemos ser. Él te necesita.

Dime que lo filmaron en cámara lenta...

-¡Aléjate o Justin Bieber muere!
-¡Ja! ¡Justin Bieber! ¡Él te llamó Justin Bieber!

Bésame como si me hubieras extrañado, Red.

-La amaba. La amaba como un océano ama el agua.
-Un océano es agua.

No sé mucho acerca de este chico Cable, pero te garantizo que no ha matado a tanta gente como el melanoma.

Siempre me horroricé por el descarado sexismo en el nombre del grupo. ¿X- Men? ¿“Men”? El punto es que nuestro grupo tendrá una visión de futuro. Genero neutral. De ahora en adelante, seremos conocidos como... X-Force.

¿Puedes hablar más alto? Es difícil escucharte con ese pene en tu boca.

Bombea los frenos de odio, Thanos.

-Domino. Soy afortunada.
-La suerte no es un superpoder. Y ciertamente no muy cinematográfica.
-Sí, lo es.
-Encontrémonos en el medio y digamos: “No. No lo es”.

¡Dios, me gustaría haber terminado la universidad!

-Nuevo plan. ¡Utiliza todos tus poderes imaginarios para evitar que Cable mate a ese niño!
-¿Dónde está él? ¡No puedo verlo!
-¡Él está encima de ti! ¡Entra por tu espalda! ¡Oh, Dios! ¡Está adentro!
-¿Te escuchas a ti mismo, verdad?
-Doble sentido accidental.

La familia siempre fue una palabra de mierda para mí.

Todos estos ancianos blancos en las paredes… debería haber traído mi silbato de violación.

Siempre ha sido mi sueño ver mi rostro reflejado en tu casco.

Creo que el dubstep nunca muere.

La familia no es una palabra de mierda. Hay una para ti. Sólo sigue buscando.

¿Una habitación de pánico, en serio? ¿Puedes salir? Verdaderamente, tengo que irme. Es mi aniversario.

-Eres mi Tom Cruise.
-Y tú eres mi Kirsten Dunst.

George Michael tenía razón. Nunca voy a bailar de nuevo. Por lo menos, queda Bowie…

-¿Cuál es tu superpoder?
-Coraje.
-Adorable.

Y es por eso que nunca comemos una estrella de mar cruda.

Una vez más, la intolerancia asoma su fea cabeza…

Así es como lo hacemos en la Madre Rusia.

Bienvenido a las Grandes Ligas.

Gracias por nada, Canadá.

Es tiempo de mirar en Linkedin.

Nací en la guerra, me crie en ella. La gente cree que entienden el dolor, pero no tienen ningún concepto de eso. ¿Cuál es el mayor dolor que has sentido alguna vez? Tal vez la clase de dolor que te hace más máquina que hombre...

No eres ningún maldito aquí, sólo eres un payaso disfrazado de juguete sexual.

-¡Hola, Yukio!
-¡Hola, Wade!

Acabo de ver el anuncio y pensé que se veía divertido.

24.5.18

la comedia continúa

DEADPOOL 2
data: https://www.imdb.com/title/tt546316

“Deadpool” (http://libretachatarra.blogspot.com.ar/2016/03/el-heroe-atipico.html) fue la sorpresa de hace un par de años. Una peculiar vuelta de tuerca sobre el cine proveniente de los cómics, con un superhéroe grosero, políticamente incorrecto, con mucho humor (y humor de grueso calibre). Para Ryan Reynolds, especialmente, un resurgir tras intercalar fracasos con películas interesantes. Todo esto era un peso muy importante a la hora de hacer la segunda parte de esta historia. Porque el riesgo de la repetición, del chiste fácil, estaba latente. Y vale decir que “Deadpool 2” supera a su antecesora. Es la película ideal para reírse mucho (pero mucho) y dejar atrás los problemas que nos acompañaron a la puerta del cine. Si el espectador se presta a este juego (con tomadas de pelo al mundo de los superhéroes y a Hollywood), va a pasar un muy buen momento. Al que no enganche con el humor negro del personaje, le recomendamos buscar otra película.

En esta etapa, nuestro héroe, Deadpool, enfrenta una nueva tragedia personal que lo hace pensar en bajar los brazos y terminar con su vida. Lo condena su habilidad: no puede morir, se regenera sin importar el grado de sus heridas. En el camino del derrumbe se cruza un niño, abusado en un internado de mutantes, que es buscado por un asesino del futuro. Deadpool se encargará no sólo de protegerlo sino de cambiarlo. En todo asesino del futuro hay un niño que todavía no conoció el sabor del crimen. Deadpool tendrá 30 segundos para demostrarle que hay una familia esperando, no importa cuál cruel haya sido la vida con uno.

Como en toda buena historia, al buscar la redención del niño, Deadpool encontrará su propia redención y sabrá que, también a él, hay una familia esperándolo.

Ahora bien, si leyeron hasta acá dirán: “esto es una telenovela”. No. Este “mensaje” está en el medio de escenas hilarantes, personajes que explotan en pedazos, chistes guarros y muchas referencias cinéfilas y de la historieta. Siempre rompiendo la cuarta pared, clonando los clichés para tomarles el pelo. Eso es lo distinto de “Deadpool 2”. Y es lo que provoca la carcajada.

Cuando se juega al límite, es fundamental el protagonista. Y Ryan Reynolds se luce, tensando la cuerda en el punto justo. El humor y la locura, el desborde, convive con la emoción y el drama. Todo mezclado, en la dosis adecuada, para pasar un muy buen momento.

Josh Brolin añade a otro villano, después de ubicarse detrás de la máscara de Thanos. Un villano que termina no siendo tan villano y tiene ecos nada disimulados de Terminator. Del muy buen elenco secundario, nos quedamos con Zazie Beetz, Domino, la morocha de pelo afro que se destaca por su buena suerte.

Entre las escenas, brillante la secuencia inicial, la presentación al estilo James Bond, el aterrizaje del equipo X-Force, el gag de las piernas de bebé, el gag autorreferencial del tiro en la cabeza tras leer el guion de “Linterna Verde”.

Disfruten las carcajadas. Mañana, las mejores frases.

23.5.18

el primer atlas mundial

(…)

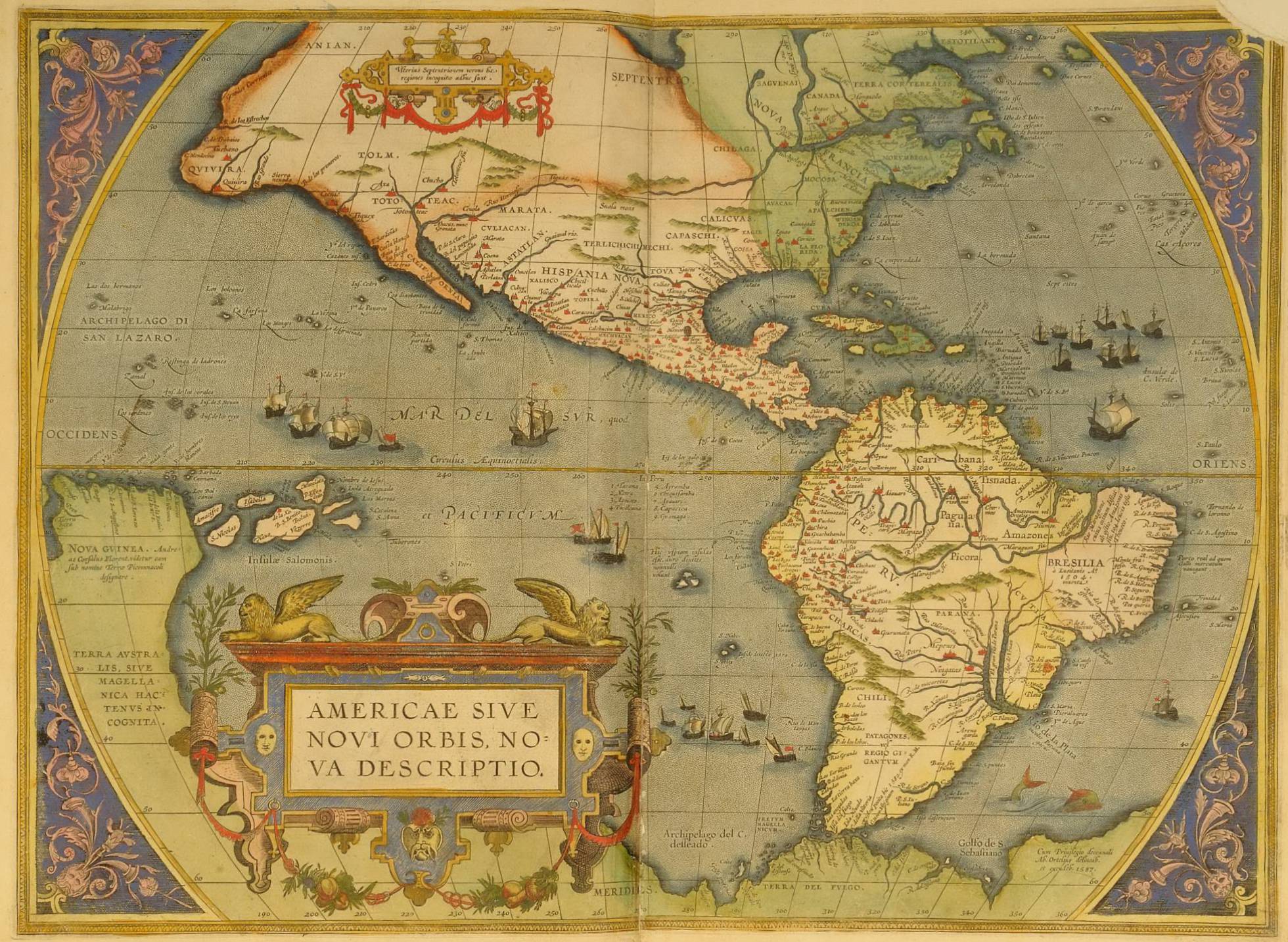
Abraham Ortelius, también escrito como Oertel, Orthellius o Wortels, nació en Amberes (Bélgica) el 14 de abril 1527 y fue criado por su tío después de la muerte de su padre junto a sus dos hermanas, Anne y Elisabeth. La familia Ortelius era originaria de Augsburgo, pero al ser acusada de protestante estuvo en continuo movimiento por miedo a la persecución.

Tras estudiar griego, latín y matemáticas, el pequeño Abraham Ortelius se estableció en su ciudad natal. Aprendió el oficio de grabador, trabajó en lo que se conocía como iluminador de mapas y en 1554 se dedicó a la venta de mapas, libros, monedas y antigüedades. Fue precisamente el mundo del comercio lo que le permitió realizar viajes extensos por toda Europa y establecer contactos con la comunidad internacional de académicos interesados en la exploración del mundo y la cartografía, especialmente con los ingleses Richard Hakluyt y John Dee. De ellos Ortelius obtuvo materiales cartográficos y gran información, al igual que hizo de su admirado colega flamenco Gerhardus Mercator, también geógrafo y quien se cree que inspiró su pasión por la creación de mapas.

Abraham Ortelius comenzó a dibujar diversos mapas en la década de 1560. Entre ellos destacan los de Egipto, Asia, Tierra Santa y el Imperio Romano. La recopilación que hacía de ellos en sus viajes le servía para repintarlos sobre lino, colorearlos y añadirles información, lo cual le fue reportando ganancias y le permitió seguir viajando.

El incipiente cartógrafo tuvo además la suerte de haber nacido en un país comerciante y exportador, con tres de los puertos marítimos más importantes del mundo y rodeado de agua, por lo que quizá Abraham Ortelius también pensó en abrir nuevas rutas marítimas y comerciales para generar riqueza con su afición convertida en profesión.

(…)

El 20 de mayo de 1570 Abraham Ortelius publicó ‘Theatrum Orbis Terrarum’, 70 mapas en 53 hojas. La obra contenía un mapa mundial y mapas de los continentes de África y Asia, así como de Europa, que fue el área más estudiada. Fue una obra que no tuvo rival en su género en toda Europa entre la primera edición de 1570 y la última, fechada en 1612, con un total de 31 ediciones en 7 lenguas diferentes: holandés (1571), alemán (1572), francés (1572), español (1588), inglés (1606) e italiano (1608). Además, vieron la luz cinco suplementos, que tituló ‘Additamenta’, entre 1573 y 1597. En 1624, ‘Theatrum’ había pasado por 40 ediciones y había crecido a 166 mapas, apareciendo incluso en latín.

(…)

Además de este interesante ‘Catalogus auctorum’ por ser la primera vez que se recogían las fuentes, a continuación Abraham Ortelius realizó un también útil ‘Index tabularum’, así como el ‘Nomenclator’ que cierra la serie de mapas y brinda las equivalencias latinas para los topónimos modernos. Los mapas están representados por barcos en medio del mar y algunos monstruos marinos como aún se consideraba en aquella época.

Sin embargo, se dice que el primer Atlas moderno fue el del mismo Mercator, amigo íntimo de Ortelius, solo que retrasó su edición, precisamente por amistad, para que resaltara el ‘Theatrum Orbis Terrarum’. Como reconocimiento a este hecho, Ortelius, por su parte, tomó los mapas de mayor relevancia de Mercator.

Según los estándares modernos, las páginas del considerado primer atlas de Abraham Ortelius están llenas de errores, aunque muchos fueron corregidos en las 25 ediciones posteriores publicadas antes de su muerte, pero si por algo también destaca el ‘Theatrum’, aparte de por ser pionero en la cartografía, es por ser la primera evidencia de que alguien consideró la deriva continental, la teoría de que los continentes alguna vez estuvieron unidos antes de separarse.

(…)

Abraham Ortelius murió en 1598 y la noticia llenó de luto público Amberes, donde ya era ampliamente reconocido por su aportación a la cartografía.

(…)

ALBERTO LÓPEZ
“Abraham Ortelius, el cartógrafo del primer atlas mundial en el siglo XVI”
(el país, 20.05.18)

22.5.18

twitter antes del Mundial

Imágenes de nuestra cuenta en Twitter: @libretachatarra

Dresden, Germany, 1945
@moodvintage

@libretachatarra

This awesome Blue Mycean Mushroom.
@i_iove_nature

@libretachatarra

Matera Basilicata - Italy
@PicPublic

@libretachatarra

The Moon by Salvador Dali
@ArtPicsChannel

@libretachatarra

La Calle Larga de Barracas (actual avenida Montes de Oca) hacia 1894. Al fondo se alcanza ver borrosa, la iglesia de Santa Felicitas.
@BsAs_recuerdo

@libretachatarra

@RaminNasibov

@libretachatarra

Betty Grable
@NotableHistory

@libretachatarra

Picture XVI, The Great Gate of Kiev. Stage set for Mussorgsky's Pictures at an Exhibition in Friedrich...
@artistkandinsky

@libretachatarra

Macau
@MariaBoedeker

@libretachatarra

Vincent Van Gogh Self Portraits
@ArtPicsChannel

@libretachatarra

@EyePleasingPorn

@libretachatarra

The Ancient Greeks played with yo-yos.
@weird_hist

21.5.18

zonda

Cuenta la leyenda que había un indio huarpe llamado Huampi notable por su destreza con el arco y la flecha. Amo y señor de toda la comarca, gobernaba varias tribus de las que ocupaban los valles Calchaquíes. Admirado y temido por todos, cazador infatigable, tenía un gran defecto, la soberbia. Se vanagloriaba de su puntería y no cesaba de matar a diestra y siniestra a cuanto animal se le cruzaba en el afán de demostrar su supremacía en tales lides. En los bosques, praderas, montes y valles que recorría, tanto caían liebres, guanacos, cóndores, vicuñas, suris, aves, vizcachas que fue dejando despoblada de animales la región. No mostraba compasión ni con las crías.

Hasta las aves huían de miedo o callaban su canto cuando se aproximaba. Pero un día se le apersonó la Pachamama entre fuertes resplandores llamándolo al orden por su descontrolado y feroz comportamiento. Le advirtió que sería severamente castigado si continuaba cazando indiscriminadamente: (sic) “¿Piensas, indio soberbio, que he creado los animales para que tú los mates? Sigue matando y llegará el momento en que te faltará su carne, su leche para alimentarte, y sus pieles para abrigarte. Si matas las vicuñas y guanacos, ¿dónde hallarás lana suave y sedosa para tejer tus mantas? Si matas las llamas, ¿quién llevará tu carga a lugares lejanos? Si matas las aves no tendrás plumas para adornarte. Eres ambicioso y egoísta. No sabes respetar ni apreciar los bienes que te da la Madre Tierra. Huampi, no tienes corazón. Tampoco mereces perdón, sino un castigo por tu maldad. Y te llegará!”. Pachamama se evaporó envuelta en su luz.

Sin embargo, Huampi, preso de su soberbia, desoyó las advertencias y redobló su rebeldía arremetiendo contra animales y crías sin ninguna compasión.

Luego de un tiempo Pachamama se apareció enfurecida por la desobediencia del joven escupiendo grandes nubarrones de polvo y arena que envolvieron por entero a Huampi, y lo condenó junto a su tribu a sufrir las embestidas de un intenso viento rastreo, caliente como el infierno que los asfixiaba en polvo sofocante, el cual provocaba incendio en los campos, las chacras, los cultivos, y cuya fuerza podía volar ranchos, techos, árboles, mataba a los viejos y trastornaba a los jóvenes.

Dicen que desde entonces, cada vez que alguien desoye a la Madre Tierra, sopla el tórrido viento zonda por nuestros valles andinos con una voz casi humana que se oye a lo lejos, traspasa la Cordillera como un suspiro de dolor, tan fuerte que hace temblar las casas y la tierra, y tiene el poder de transformar el clima, la geografía y los hombres.

(…)

GLADYS ABILAR
“El terrible viento que nació por enfurecer a la Pachamama”
(la nación, 19.05.18)

19.5.18

reporte de noticias: semana del 15/05

“El Mapa de las Antípodas: el sitio web que te permite saber en qué lugar de la Tierra aparecerías si cavaras un túnel bajo tus pies”
(bbc mundo, 18.05.18)
http://www.bbc.com/mundo/noticias-44148969

“Joya de Cerén, el extraordinario sitio precolombino en el El Salvador que fue cubierto por la erupción de un volcán hace 1.400 años y sigue intacto”
(bbc mundo, 17.05.18)
http://www.bbc.com/mundo/noticias-america-latina-43926448

“El monstruoso agujero negro que se traga un sol cada dos días”
(bbc mundo, 17.05.18)
http://www.bbc.com/mundo/noticias-44153904

“El hábito sexual suicida que tiene a un par de especies de marsupiales en riesgo de extinción”
(bbc mundo, 16.05.18)
http://www.bbc.com/mundo/noticias-44146281

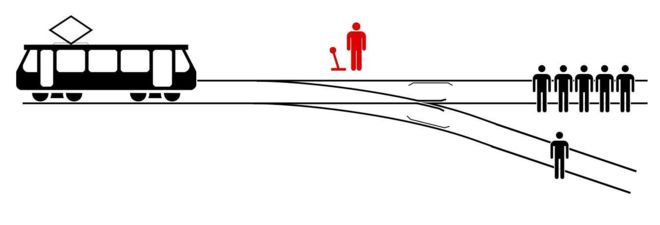
“El dilema del tranvía: el experimento sicológico que cuestiona qué tan buenas o malas son tus decisiones”
(bbc mundo, 16.05.18)
http://www.bbc.com/mundo/noticias-44133313