Un problema que, transcurridos más de cincuenta años, todavía no ha sido resuelto satisfactoriamente… Al menos desde un punto de vista matemático. Es decir, donde la solución venga acompañada de una prueba matemática que la acredite como única e insuperable. Mientras ésta no se alcance, se tratará de una mera conjetura susceptible de ser invalidada, vulnerada y superada en cualquier momento.
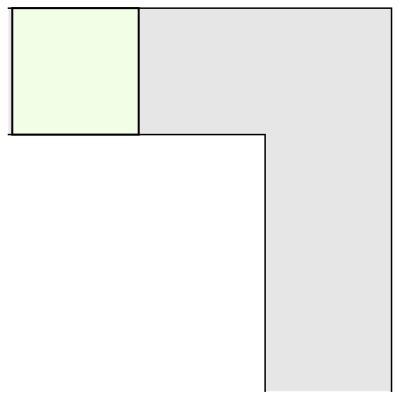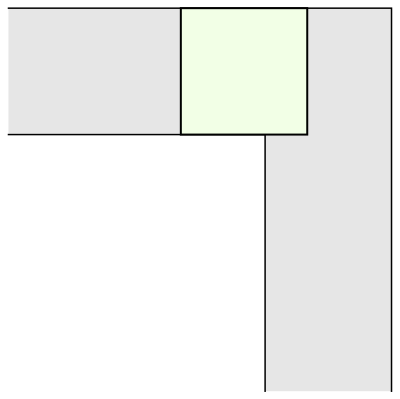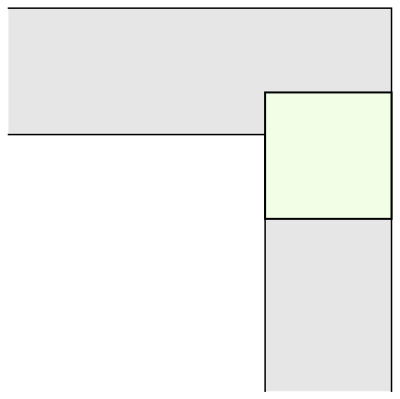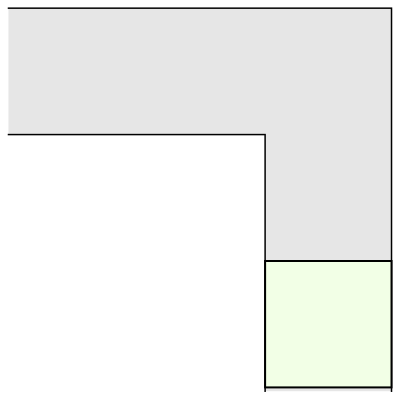
La primera e inmediata respuesta fue la de un sofá cuadrado de 1 metro de lado (y por tanto, de superficie 1 metro cuadrado). Que, también de inmediato, fue superada por la de un sofá semicircular de radio 1 (de superficie π/2 = 1,57 metros cuadrados), que permite girar perfectamente en la esquina —siempre en un plano horizontal o en dos dimensiones.
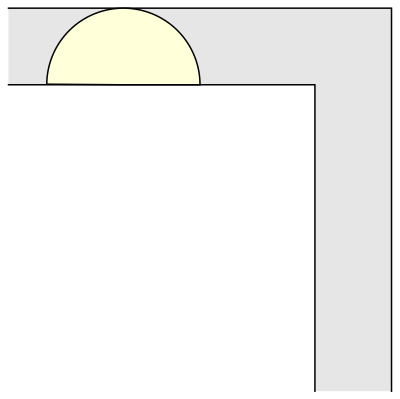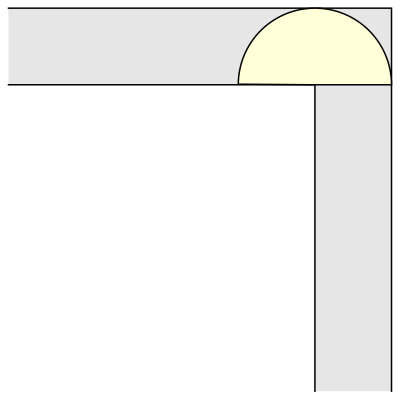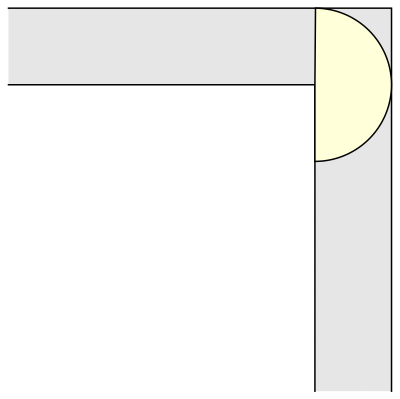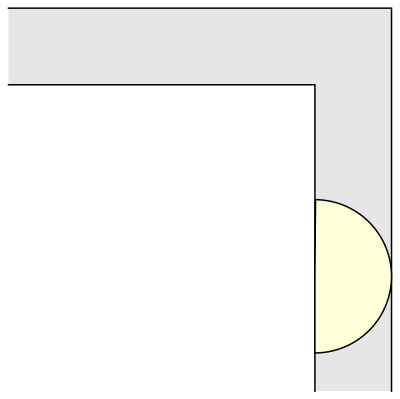
En 1968 el matemático John Hammersley enunció que una forma tipo puente o de auricular de los teléfonos de la época, con un radio = 2/π ofrecía un área máxima de 2/π + π/2 = 2,2074 metros cuadrados. Pero no lo demostró matemáticamente. Lo que dejaba la puerta abierta a que otros matemáticos siguiesen buscando una solución definitiva o, cuando menos, la prueba que demostrase que la de Hammersley lo era. Durante las siguientes dos décadas se aceptó que ésta era la forma óptima.
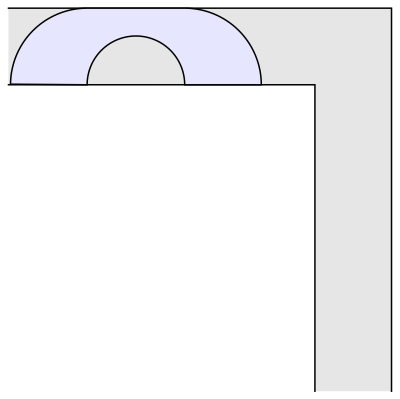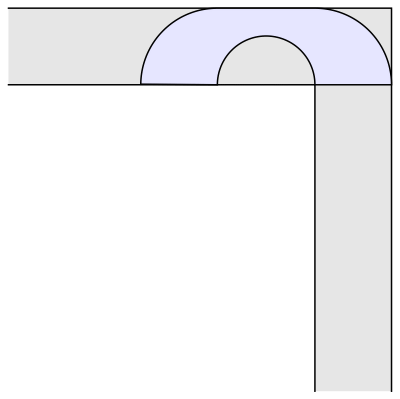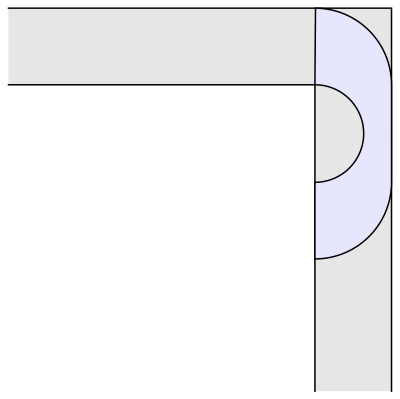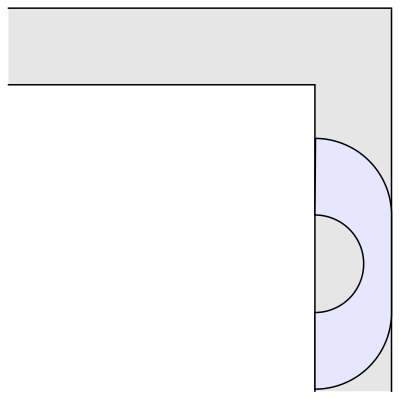
Pero entonces, en 1992, el matemático Joseph Gerver encontró una forma aún mejor, al redondear los bordes internos y alcanzando así un área ligeramente mayor, de 2,2195 metros cuadrados. Que es la respuesta que actualmente permanece vigente… aunque, nuevamente, sólo se trate de una conjetura al no existir una demostración concluyente.
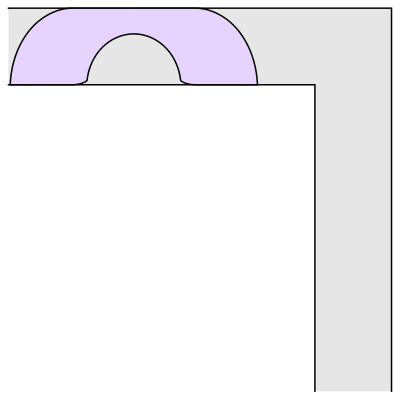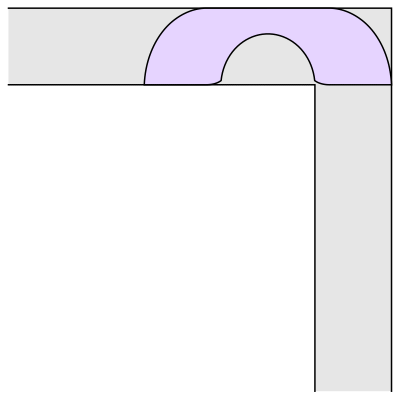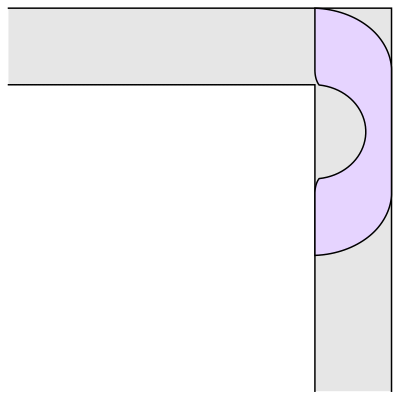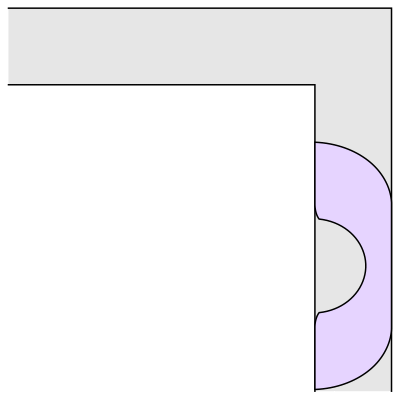
(…)
“Érase una vez un sofá en un pasillo…”
(open mind, 21.08.17)








No hay comentarios.:
Publicar un comentario